Matriks Matematika

-
Penjumlahan dan Pengurangan Matriks

A=    2  5     dan B=   4  6        Maka, A+B =    2  5    +    4  6     =    2+4  5+6    =    6  11
      ⎨6  9 ⎬              ⎨5  3 ⎬                           ⎨6  9 ⎬    ⎨5  3 ⎬     ⎨6+5  9+3⎬    ⎨11 12 ⎬

                                                             A-B =   2  5      -    4  6     =    2-4   5-6     =    -2  -1
                                                                        ⎨6  9 ⎬    ⎨5  3 ⎬     ⎨6-5   9-3 ⎬    ⎨  1   6 ⎬

Perkalian Matriks

A.B ≠  B.A  

Pembuktian :    A.B =   2  5    .   4  6     =   (2.4 + 5.5)  (2.6 + 5.3)    =   33  27
                                   ⎨6  9 ⎬  ⎨5  3 ⎬    ⎨(6.4 + 9.5)  (6.6 + 9.3)⎬    ⎨69  63⎬

                          B.A =   4  6    .   2  5     =   (4.2 + 6.6)  (4.5 + 6.9)    =   44  74
                                   ⎨5  3 ⎬  ⎨6  9 ⎬    ⎨(5.2 + 3.6)  (5.5 + 3.9)⎬    ⎨28  37⎬
Perkalian matriks menggunakan metode BASKOM (baris kali kolom)











Determinan Matriks Ordo 2 x 2
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
Nilai determinan A disimbolkan dengan 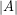\left| A \right|, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
  \[ det(A) \; = \; \left| A \right| = ad - bc \]

Contoh Soal:
Tentukan nilai determinan matriks
  \[ A \; = \; \begin{bmatrix} 3 & 1 \\ 2 & 5 \end{bmatrix} \]
Pembahasan:
  \[ \left| A \right| = ad - bc = 3 \cdot 5 - 1 \cdot 2 = 15 - 2 = 13\]

Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.

Contoh perhitungan determinan pada matriks ordo 3:
  \[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]
Maka,
  \[ \left| \textrm{A} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]
  \[ \left| \textrm{A} \right| \; = 1\cdot 3 \cdot 2 + 2 \cdot 1 \cdot 2 + 1 \cdot 3 \cdot 1 - 2 \cdot 3 \cdot 1 - 1 \cdot 1 \cdot 1 - 2 \cdot 3 \cdot 2 \]
  \[ \left| \textrm{A} \right| \; = 6 + 4 + 3 - 6 - 1 - 12 \]
  \[ \left| \textrm{A} \right| \; = -6 \]
Invers Matriks Ordo 2 x 2
Invers dari suatu matirks A
  \[ \textrm{A} \; = \; \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
dinyatakan dalam rumus di bawah.
Diketahui:
  \[ \textrm{A} \; = \; \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \]
Tentukan invers dari matrik A!
Pembahasan:
  \[ \textrm{A}^{-1} \; = \; \frac{1}{3 \cdot 4 - 2 \cdot 1} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{12 - 2} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \frac{1}{10} \begin{bmatrix} 4 & -2 \\ -1 & 3 \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{4}{10} & -\frac{2}{10} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]
  \[ \textrm{A}^{-1} \; = \; \begin{bmatrix}\frac{2}{5} & -\frac{1}{5} \\ -\frac{1}{10} & \frac{3}{10} \end{bmatrix} \]

Komentar

Posting Komentar

Postingan populer dari blog ini

Cara kerja otot SINERGIS dan ANTAGONIS

-
Gambar
CARA KERJA OTOT SINERGIS DAN ANTAGONIS   A.Secara Sinergis Otot ini sering kali disebut dengan otot protagonis,yang ketika berkontraksi menimbulkan gerak searah.         Contoh gerak otot sinergis: Pronator teres dan Pronator kuadratus (Gerakan berputar).Bila keduanya berkontraksi, telapak tangan akan melungkup. Sirkumduksi.Gabungan gerakan fleksi,abduksi,adduksi,dan ektensi yang menyebabkan gerakan melingkar.    B.Secara Antagonis Pasangan otot yang melakukan gerak berlawanan terhadap otot yang sedang melakukan kontraksi.          Contoh gerak otot Antagonis: Ekstensi - Fleksi. Ekstensi adalah gerakan meluruskan, sedangkan Fleksi adalah gerakan membengkokan. Abduksi - Adduksi. Abduksi adalah gerakan menjauhi badan,sedangkan adduksi adalah gerakan mendekati badan. Depresi - Elevansi. Depresi adalah gerak menurunkan,sedangkan Elevansi adalah gerakan mengangkat. Supinasi - Pronasi. Supinasi adalah gerak mengadahkan tangan,sedangkan pronasi
Baca selengkapnya

PROSES PEMBENTUKAN URINE

-
Gambar
  Assallamu'alaikum. Jumpa lagi setelah beberapa minggu tidak memposting. Kali ini saya akan berbagi ilmu tentang Proses Pembentukan Urine. Urine merupakan salah satu cairan hasil sisa metabolisme tubuh yang diekresikan oleh Ginjal. Tujuan pengekskresian urin adalah untuk membuang molekul-molekul sisa dalam darah yang di saring oleh ginjal dan untuk menjaga homeostatis cairan tubuh   STRUKTUR GINJAL Korteks, adalah bagian utama ginjal.Tempat inilah yang menjadi muara asalnya urin berasal. Di dalam korteks terdapat jutaan nefron nefron yang di dalamnya terletak badan Malpighi. Setiap badan Malpighi tersusun atas glomerulus, kapsula bowman, serta beberapa tubulus tubulus pendukung untuk proses pemfilteran. Darah manusia akan mulai di filter pada bagian ini. Mendula,  merupakan jaringan yang berbentuk seperti piramida piramida dimana terletak lengkung henle. Medulla adalah tempat berkumpulnya pembuluh darah kapiler dan juga kapsul bowman. Di tempat ini urin primer akan meng
Baca selengkapnya

EXPLANATION TEXT bahasa Inggris SMA/SMK

-
Gambar
Explanation Text   Explanation is a text which tells processes relating to forming of natural,social,scientific and cultural phenomena.  Explanasi adalah sebuah teks yang berisi tentang proses-proses yang berhubungan dengan fenomena-fenomena alam,sosial,ilmu pengetahuan,budaya dan lainya. FUNCTION   To explain the processes involved in the formation or working of natural or socio-cultural phenomena.  Tujuanya adalah umtuk menerangkan proses-proses yang terjadi dalam pembentukan sesuatu yang terkait dengan fenomena-fenomena alam,sosial,ilmu pengetahuan,budaya dan lainya. GENERIC STRUCTURE   General Statement. Penjelasan umum mengenai fenomena.  Sequenced of explanation. Explain the preoces of phenomena with 'why' and 'how'. Berisi tentang penjelasan proses mengapa dan bagaimana fenomena itu terjadi. Closing  LANGUAGE FEATURE  Usually comes from the author's question of 'why'and'how' of an existing phenomenon The materia
Baca selengkapnya